백준 1010 | 다리 놓기

Problem 💻

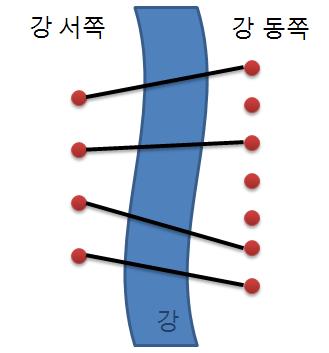
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)

재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.

입력

입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.

출력

각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.

예제 입력 1 복사

3
2 2
1 5
13 29

예제 출력 1 복사

1
5
67863915

---

Approach 1 ⭕

이 문제를 보고는 다리 M개 중 N개를 선택하는 문제라 생각하여 조합을 바로 떠올릴 수 있었다. 조합을 구현할 때는 오버플로우를 고려하여 나눗셈을 같이 하고 자료형을 long long으로 맞춰줬어야 하였다. 구현 후 바로 적용을 해보니 문제 없이 풀 수 있었다.

다만 이후에 해당 풀이 방식 외에도 DP방식으로 해결 가능하다는 것을 알게 되었고 DP 방식으로도 해결 해보았다.

세가지 방식으로 풀어 보면서 DP방식들에는 필요 없는 데이터가 추가되는 등의 단점이 존재한다는 사실을 알 수 있었다. 또한 단순한 곱셈 방식의 조합 문제이므로 해당 문제는 조합으로 푸는 것이 맞다는 생각이 들었다.

---

Solution 💡

using namespace std;

#include <iostream>
#include <vector>

//nCr
long long Combination(int n, int r)
{
	if (r > n - r)
	{
		r = n - r;
	}

	long long result = 1;
	for (int i = 1; i <= r; ++i)
	{
		// 분자 분모를 동시에 계산
		result *= n - r + i;
		result /= i;
	}

	return result;
}

long long TopDown(vector<vector<long long>>& dp, int m, int n)
{
	if (n == 0 || m == n) 
	{
		return 1;
	}
	
	if (dp[m][n] != 0) 
	{
		return dp[m][n]; // 메모이제이션
	}

	return dp[m][n] = TopDown(dp, m - 1, n - 1) + TopDown(dp, m - 1, n);
}

void BottomUp(std::vector<std::vector<long long>>& dp)
{
	for (int m = 0; m <= 30; ++m)
	{
		for (int n = 0; n <= 30; ++n)
		{
			if (n > m)
			{
				break;
			}
			else if (n == m || m == 0 || n == 0)
			{
				dp[m][n] = 1;
				continue;
			}

			dp[m][n] += dp[m - 1][n - 1] + dp[m - 1][n];
		}
	}
}

int main()
{
	int T;
	cin >> T;

	// dp[m][n] -> M, N 경우의 수
	//vector<vector<long long>> dp(31, vector<long long>(31, 0));

	//BottomUp(dp);

	for (int i = 0; i < T; ++i)
	{
		int N, M;

		cin >> N >> M;

		cout << Combination(M, N) << '\n'; // 조합
		//cout << TopDown(dp, M, N) << '\n'; // TopDown
		//cout << dp[M][N] << '\n'; //BottomUp
	}
}

---

Reference 📄

https://www.acmicpc.net/problem/1010