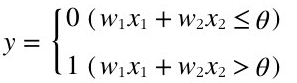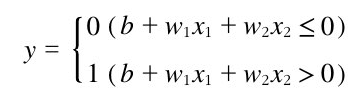밑바닥부터 시작하는 딥러닝 1 | 퍼셉트론
밑바닥부터 시작하는 딥러닝 1 Chapter 2 정리
책 정보 📖
- 책 제목: 밑바닥부터 시작하는 딥러닝 1
- 글쓴이: 사이토 고키
- 옮긴이: 개앞맵시
- 출판사: 한빛미디어
- 발행일: 2025년 01월 24일
- 챕터: Chapter 2. 퍼셉트론
책소개
딥러닝 분야 부동의 베스트셀러! 머리로 이해하고 손으로 익히는 가장 쉬운 딥러닝 입문서 이 책은 딥러닝의 핵심 개념을 ‘밑바닥부터’ 구현해보며 기초를 한 걸음씩 탄탄하게 다질 수 있도록 도와주는 친절한 안내서입니다. 라이브러리나 프레임워크에 의존하지 않고 딥러닝의 기본 개념부터 이미지 인식에 활용되는 합성곱 신경망(CNN)까지 딥러닝의 원리를 체계적으로 설명합니다. 또한 복잡한 개념은 계산 그래프를 활용해 시각적으로 전달하여 누구나 쉽게 이해할 수 있습니다. 이 책은 딥러닝에 첫발을 내딛는 입문자는 물론이고 기초를 다시금 다지고 싶은 개발자와 연구자에게도 훌륭한 길잡이가 되어줄 것입니다.
주요 내용
퍼셉트론: 딥러닝의 시작점
딥러닝을 이해하기 위해서는 반드시 알아야 할 기초 개념이 있다. 바로 퍼셉트론(Perceptron)이다. 퍼셉트론은 신경망과 딥러닝의 기초가 되는 알고리즘으로, 복잡한 인공신경망의 출발점이 된다.
퍼셉트론이란?
퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력하는 간단한 구조다. 마치 우리 뇌의 뉴런이 여러 신호를 받아 하나의 결정을 내리는 것과 유사하다.
입력이 2개인 퍼셉트론
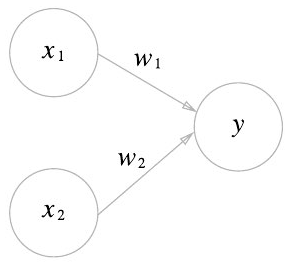
퍼셉트론의 구성 요소
퍼셉트론은 다음과 같은 요소들로 구성된다:
- x1, x2: 입력 신호
- w1, w2: 가중치(Weight) - 각 입력 신호의 중요도를 나타낸다
- 원(○): 뉴런 또는 노드라고 부른다
- 임곗값(θ): 뉴런이 활성화되는 기준값
퍼셉트론의 동작 원리는 간단하다. 입력 신호들과 가중치의 곱의 합이 임곗값을 넘어서면 1을 출력하고, 그렇지 않으면 0을 출력한다. 이때 출력이 1인 상태를 ‘뉴런이 활성화한다’고 표현한다.
퍼셉트론으로 논리 게이트 구현하기
퍼셉트론의 힘은 논리 회로를 구현할 수 있다는 점에서 드러난다. AND, OR, NAND 게이트는 모두 같은 퍼셉트론 구조를 가지며, 매개변수(가중치와 임곗값)의 값만 다르다.
AND 게이트 구현
1
2
3
4
5
6
7
8
9
10
11
12
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
else:
return 1
print(AND(0, 0)) # 0
print(AND(0, 1)) # 0
print(AND(1, 0)) # 0
print(AND(1, 1)) # 1
편향(Bias) 도입
임곗값 θ를 -b로 바꾸면 수식이 더 간단해진다. 이때 b를 편향(Bias)이라 한다.
편향을 사용한 구현:
1
2
3
4
5
6
7
8
9
10
11
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
편향과 가중치의 차이점:
- 편향: 뉴런이 얼마나 쉽게 활성화하느냐를 조정하는 매개변수
- 가중치: 입력 신호가 결과에 주는 영향력을 조절하는 매개변수
다양한 논리 게이트 구현
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5]) # AND와 반대 부호
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2 # AND보다 작은 임곗값
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
전부 가중치와 편향 값만 다른 것을 알 수 있다
단층 퍼셉트론의 한계
하지만 퍼셉트론에는 치명적인 한계가 있다. XOR 게이트(배타적 논리합)를 표현할 수 없다는 것이다.
OR의 경우 다음처럼 직선으로 영역 표현 가능
XOR은 직선 하나로는 영역을 표현 불가능
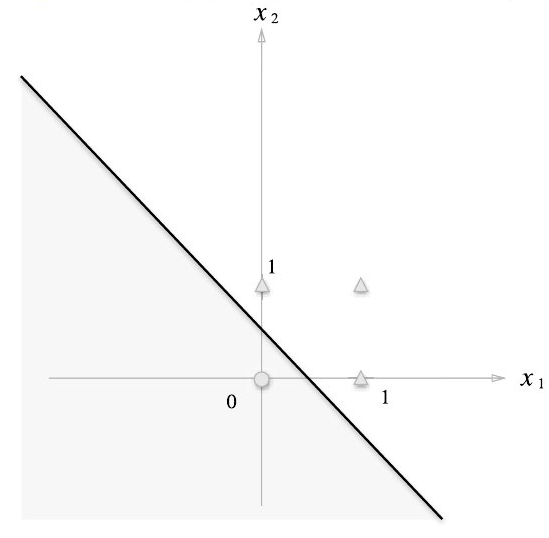
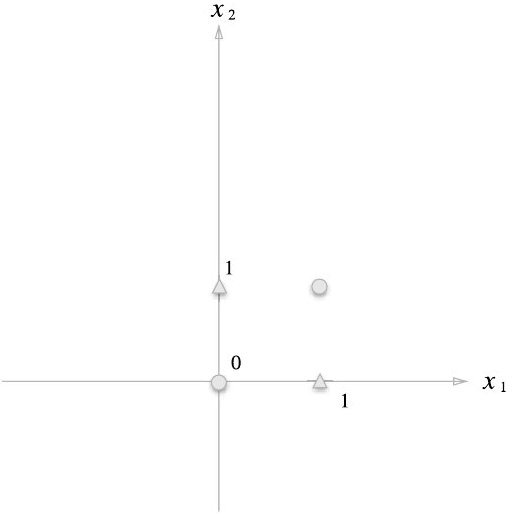
퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있다. OR 게이트는 직선 하나로 0과 1 영역을 구분할 수 있지만, XOR 게이트는 곡선이나 복잡한 경계가 필요하다.
다층 퍼셉트론(MLP): 한계를 뛰어넘다
이 문제는 다층 퍼셉트론으로 해결할 수 있다. 층을 쌓아서 더 복잡한 표현이 가능하다.
XOR 게이트 구현
XOR 게이트는 기존의 논리 게이트들을 조합하여 만들 수 있다:
1
2
3
4
5
6
7
8
9
10
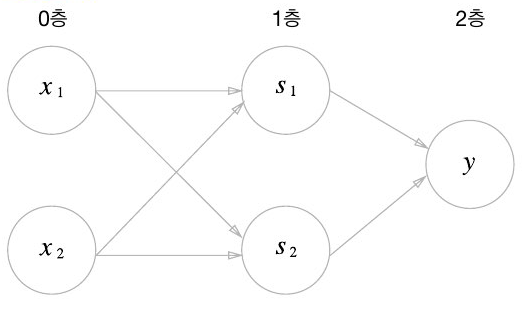
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
print(XOR(0, 0)) # 0
print(XOR(0, 1)) # 1
print(XOR(1, 0)) # 1
print(XOR(1, 1)) # 0
XOR의 퍼셉트론
XOR은 2층 퍼셉트론으로 구현된다. 단층 퍼셉트론으로는 불가능했던 것이 층을 하나 늘리니 가능해진 것이다.
퍼셉트론의 무한한 가능성
다층 퍼셉트론의 잠재력은 놀랍다:
복잡한 회로 구현
- 가산기: 덧셈을 처리하는 회로
- 인코더: 2진수를 10진수로 변환하는 회로
- 컴퓨터: 이론상 2층 퍼셉트론만으로도 컴퓨터를 만들 수 있다
이론적 기반
NAND 게이트의 조합만으로 컴퓨터가 수행하는 모든 일을 재현할 수 있다. 이는 퍼셉트론으로도 컴퓨터를 표현할 수 있음을 의미한다. 특히 비선형인 시그모이드 함수를 활성화 함수로 사용하면 임의의 함수를 표현할 수 있다는 사실이 수학적으로 증명되었으며 이론상 2층 퍼셉트론으로 컴퓨터를 만들 수 있다는 사실을 뒷받침하였다.
마무리
퍼셉트론은 간단해 보이지만 딥러닝의 핵심 아이디어를 담고 있다. 층을 거듭 쌓으면 비선형적인 표현이 가능하고, 이론상 컴퓨터가 수행하는 모든 처리를 표현할 수 있다.
단층 퍼셉트론의 한계를 다층 퍼셉트론으로 극복하는 과정은 딥러닝 발전사의 중요한 이정표다. 이 기초 개념을 확실히 이해하면 더 복잡한 신경망 구조도 쉽게 받아들일 수 있을 것이다.