밑바닥부터 시작하는 딥러닝 1 | 신경망 학습 2

밑바닥부터 시작하는 딥러닝 1 Chapter 4 정리

게시 2025/09/08

By Shin Min Geun

15 분읽는 시간

책 정보 📖

책 제목: 밑바닥부터 시작하는 딥러닝 1
글쓴이: 사이토 고키
옮긴이: 개앞맵시
출판사: 한빛미디어
발행일: 2025년 01월 24일
챕터: Chapter 4. 신경망 학습

책소개

딥러닝 분야 부동의 베스트셀러! 머리로 이해하고 손으로 익히는 가장 쉬운 딥러닝 입문서 이 책은 딥러닝의 핵심 개념을 ‘밑바닥부터’ 구현해보며 기초를 한 걸음씩 탄탄하게 다질 수 있도록 도와주는 친절한 안내서입니다. 라이브러리나 프레임워크에 의존하지 않고 딥러닝의 기본 개념부터 이미지 인식에 활용되는 합성곱 신경망(CNN)까지 딥러닝의 원리를 체계적으로 설명합니다. 또한 복잡한 개념은 계산 그래프를 활용해 시각적으로 전달하여 누구나 쉽게 이해할 수 있습니다. 이 책은 딥러닝에 첫발을 내딛는 입문자는 물론이고 기초를 다시금 다지고 싶은 개발자와 연구자에게도 훌륭한 길잡이가 되어줄 것입니다.

출처 : 밑바닥부터 시작하는 딥러닝 1 - 교보문고

주요 내용

경사법: 최적화의 핵심 알고리즘
손실 함수를 정의했다면 이제 그 값을 최소화하는 매개변수를 찾아야 한다. 이를 위해 수치 미분과 경사법이라는 개념들을 사용한다. 복잡한 함수에서 최적해를 찾아가는 과정을 살펴본다.

수치 미분: 컴퓨터로 미분하기

해석적 미분 vs 수치 미분

미분을 계산하는 방법은 크게 두 가지가 있다:

해석적 미분:

수식을 전개해서 미분하는 일반적인 방법
예: $y = x^2$ → $\frac{dy}{dx} = 2x$
정확한 값을 구할 수 있다

수치 미분:

아주 작은 차분으로 미분하는 방법
근사치로 계산하지만 해석적 미분과 거의 비슷한 수준의 작은 오차를 보인다
컴퓨터로 구현하기 쉽다

수치 미분 구현하기

잘못된 구현 예:

  
def numerical_diff(f, x):
    h = 1e-50  # 너무 작은 값
    return (f(x + h) - f(x)) / h

문제점:

반올림 오차: 너무 작은 h 값으로 인해 정확한 표현이 불가능
h는 $10^{-4}$ 정도가 적절하다고 알려져 있다

개선된 구현:

  
def numerical_diff(f, x):
    h = 1e-4  # 0.0001
    return (f(x + h) - f(x - h)) / (2 * h)

개선 사항:

적절한 h 값: $10^{-4}$ 사용
중심 차분: $(x+h)$와 $(x-h)$를 이용해 오차 감소
- 기존 $(x+h)$와 $x$의 차분은 전방 차분이라고 한다

편미분: 다변수 함수의 미분

편미분의 개념

변수가 여러 개인 함수에 대한 미분을 편미분이라고 한다.

  
def function_2(x):
    return x[0]**2 + x[1]**2

이 함수의 편미분은 $\frac{\partial f}{\partial x_0}$, $\frac{\partial f}{\partial x_1}$로 표현되며, 목표 변수 하나에 초점을 맞추고 다른 변수는 상수로 고정하여 구한다.

기울기: 모든 편미분의 집합

기울기의 정의

모든 변수의 편미분을 벡터로 정리한 것을 기울기(Gradient)라고 한다:

\[\nabla f = \left(\frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1}\right)\]

기울기 계산 구현

  
def numerical_gradient(f, x):
	h = 1e-4
	# x와 형상이 같은 배열을 생성한다. (0으로 초기화 된다.)
	# x.shape = (2,3)이면 grad는 (2,3)의 형상을 가지고 모든 값이 0.
	grad = np.zeros_like(x)
	
	for idx in range(x.size):
		tmp_val = x[idx]
		
		# f(x+h) 계산
		x[idx] = tmp_val + h
		fxh1 = f(x)
		
		# f(x-h) 계산
		x[idx] = tmp_val - h
		fxh2 = f(x)
		
		# 수치 미분
		grad[idx] = (fxh1 - fxh2) / (2 * h)
		x[idx] = tmp_val # 값 복원
		
numerical_gradient(function_2, np.array([3.0, 4.0])) # array([6, 8])
numerical_gradient(function_2, np.array([0.0, 2.0])) # array([0, 2])
numerical_gradient(function_2, np.array([3.0, 0.0])) # array([3, 0])

개선 버젼

  
def function_2_improve(x): 
	return np.sum(x**2)

def numerical_gradient(f, x):
	h = 1e-4
	grad = np.zeros_like(x, dtype=float)
	
	# 일종의 numpy 이터레이터
	# N차원 배열(그리고 여러 배열을 동시에) 일관된 순서로 순회하는 범용 이터레이터로,
	# 2D/3D에서도 중첩 for문을 한 루프로 단순화할 수 있다.
	it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
	while not it.finished:
		idx = it.multi_index
		tmp_val = x[idx]
		
		# f(x+h)
		x[idx] = tmp_val + h
		fxh1 = f(x)

		# f(x-h)
		x[idx] = tmp_val - h
		fxh2 = f(x)

		# 수치 미분
		grad[idx] = (fxh1 - fxh2) / (2 * h)
		x[idx] = tmp_val  # 값 복원

		it.iternext()
	return grad

X = np.array([[3.0, 4.0], [0.0, 2.0], [3.0, 0.0]])
grad = numerical_gradient(function_2_improve, X) # 3개를 묶어서 처리가 가능해졌다.

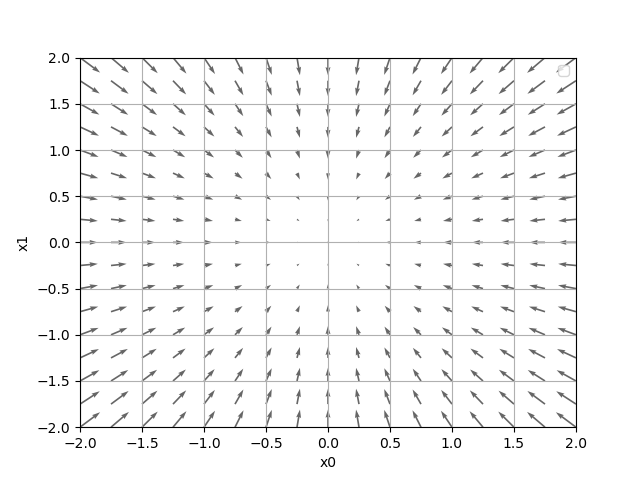
기울기의 시각화

코드

  
# 기존 코드는 X, Y를 따로 받아서 2번 거치는 과정이 있었는데 numerical_gradient 한번으로 끝나도록 수정함
if __name__ == '__main__':
	x0 = np.arange(-2, 2.5, 0.25) # 좌표 1 18사이즈의 -2~2.5 일차원 행렬
	x1 = np.arange(-2, 2.5, 0.25) # 좌표 2
	print(x0.size)
	print(x1.size)
	X, Y = np.meshgrid(x0, x1) # 1차원 좌표 벡터들로 좌표 격자 행렬을 만든다.
	# X => 18x18크기 -2~2.5값을 가지는 행백터가 18개 
	# X[0] = [-2.   -1.75 -1.5  -1.25 -1.   -0.75 -0.5  -0.25  0.    0.25  0.5   0.75   1.    1.25  1.5   1.75  2.    2.25]
	# Y => 18x18크기 -2~2.5값을 가지는 열백터가 18개 
	# Y[0] = [-2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2.]
	# Y값이 고정되고 X값이 계속바뀌는 느낌이다.

	X = X.flatten() # 다차원을 1차원으로 만든다.
	Y = Y.flatten()
	# np.array([X, Y]) (2, 324) 행렬 반환 C[0][?]가 x좌표 C[1][?]가 y좌표 역할
	C = np.array([X, Y]).T # 전치를 적용해서 (324, 2)로 수정하여 C[x][0] C[x][1] 이 한쌍이 되도록
	grad = numerical_gradient(function_2, C)
	
	# 그래프를 그린다.
	#  -grad[: 0], -grad[: 1] -> 각 열을 좌표로 설정
	plt.figure()
	plt.quiver(X, Y, -grad[: 0], -grad[: 1],  angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
	plt.xlim([-2, 2])
	plt.ylim([-2, 2])
	plt.xlabel('x0')
	plt.ylabel('x1')
	plt.grid()
	plt.legend() 
	plt.draw()
	plt.show()

기울기의 특성:

기울기는 각 지점에서 함수값이 가장 크게 감소하는 방향을 가리킨다
화살표는 함수의 출력값을 가장 크게 줄이는 방향을 나타낸다
기울기가 0인 지점이 최솟값이 될 가능성이 높다

경사법: 최적화의 핵심

경사법의 필요성

머신러닝 문제에서는 학습 단계에서 최적의 매개변수를 찾아야 한다. 최적이란 손실 함수가 최솟값이 될 때의 매개변수 값이다.

하지만 일반적인 문제의 손실 함수는 매우 복잡해서 어디가 최솟값인지 직접 알기 어렵다. 이때 경사법(Gradient Descent)을 사용한다.

경사법의 원리

기본 아이디어:

현재 위치에서 기울기 방향으로 일정 거리 이동
이동한 위치에서 다시 기울기를 구해 이동
이 과정을 반복하여 함수값을 점차 줄여나간다

수식: $x_0 = x_0 - \eta \frac{\partial f}{\partial x_0}$ $x_1 = x_1 - \eta \frac{\partial f}{\partial x_1}$

$\eta$(eta): 갱신하는 양을 나타내며 학습률(Learning Rate)이라고 한다
한 번의 학습으로 매개변수 값을 얼마나 갱신할지를 정한다

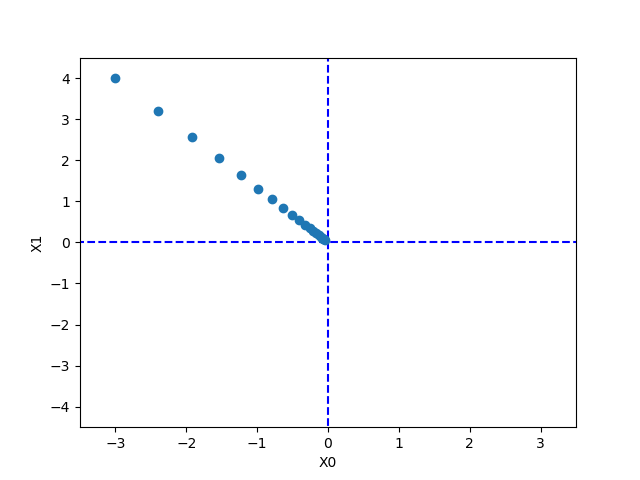
경사 하강법 구현

  
def gradient_descent(f, init_x, lr=0.01, step_num=100):
    x = init_x
    
    for i in range(step_num):
        grad = numerical_gradient(f, x)
        x -= lr * grad  # 기울기에 학습률을 곱한 값만큼 x를 이동
    
    return x

매개변수 설명:

f: 최적화하려는 함수(손실 함수)
init_x: 초기값
lr: 학습률
step_num: 경사법 반복 횟수

학습률의 중요성

학습률 설정은 경사법의 성공 여부를 좌우한다:

학습률이 너무 클 때:

갱신량이 커서 최솟값을 지나쳐 발산할 수 있다
값이 진동하며 수렴하지 않는다

학습률이 너무 작을 때:

갱신이 거의 이루어지지 않는다
학습 시간이 과도하게 길어진다
지역 최솟값에 빠질 위험이 증가한다

경사법의 한계

지역 최솟값 문제:

복잡한 함수에서는 기울기가 가리키는 방향에 전역 최솟값이 없는 경우가 대부분
기울기가 0인 곳이 극솟값이거나 안정점일 가능성이 크다
고원(Plateau): 평평한 곳에서 학습이 진행되지 않는 정체기

그럼에도 불구하고:

기울기 정보는 여전히 함수값을 줄이는 최선의 방향을 제시한다
실제로 많은 문제에서 좋은 해를 찾을 수 있다

하이퍼파라미터

매개변수 vs 하이퍼파라미터

매개변수(Parameters):

가중치와 편향 같은 신경망의 학습 가능한 변수
훈련 데이터와 학습 알고리즘을 통해 자동으로 획득

하이퍼파라미터(Hyperparameters):

학습률, 에포크 수, 배치 크기 등
사람이 직접 설정해야 하는 매개변수
모델의 학습 과정을 제어한다

하이퍼파라미터 튜닝의 중요성

적절한 하이퍼파라미터 설정은 학습 성공의 핵심이다:

학습률: 너무 크면 발산, 너무 작으면 느린 수렴
배치 크기: 메모리 사용량과 학습 안정성의 트레이드오프
에포크 수: 과소적합과 과대적합의 균형

하이퍼파라미터는 보통 여러 값을 시도해보며 가장 좋은 성능을 내는 값을 선택한다.

마무리

경사법은 신경망 학습의 핵심 알고리즘이다. 수치 미분을 통해 기울기를 계산하고, 그 방향으로 조금씩 이동하며 최적해를 찾아간다.

핵심 포인트:

수치 미분: 컴퓨터로 구현 가능한 미분 방법
기울기: 함수값이 가장 크게 감소하는 방향을 제시
경사법: 기울기를 따라 이동하며 최적해를 탐색
학습률: 학습 속도와 안정성을 결정하는 중요한 하이퍼파라미터

다음 단계에서는 이 개념들을 실제 신경망에 적용하여 매개변수를 학습시키는 방법과 예제를 살펴본다.

Study, Study\DeepLearning

AI Deep Learning Python Book Note