밑바닥부터 시작하는 딥러닝 1 | 오차역전파법 1
밑바닥부터 시작하는 딥러닝 1 Chapter 5 정리
책 정보 📖
- 책 제목: 밑바닥부터 시작하는 딥러닝 1
- 글쓴이: 사이토 고키
- 옮긴이: 개앞맵시
- 출판사: 한빛미디어
- 발행일: 2025년 01월 24일
- 챕터: Chapter 5. 오차역전파법
책소개
딥러닝 분야 부동의 베스트셀러! 머리로 이해하고 손으로 익히는 가장 쉬운 딥러닝 입문서 이 책은 딥러닝의 핵심 개념을 ‘밑바닥부터’ 구현해보며 기초를 한 걸음씩 탄탄하게 다질 수 있도록 도와주는 친절한 안내서입니다. 라이브러리나 프레임워크에 의존하지 않고 딥러닝의 기본 개념부터 이미지 인식에 활용되는 합성곱 신경망(CNN)까지 딥러닝의 원리를 체계적으로 설명합니다. 또한 복잡한 개념은 계산 그래프를 활용해 시각적으로 전달하여 누구나 쉽게 이해할 수 있습니다. 이 책은 딥러닝에 첫발을 내딛는 입문자는 물론이고 기초를 다시금 다지고 싶은 개발자와 연구자에게도 훌륭한 길잡이가 되어줄 것입니다.
주요 내용
- 오차역전파법: 효율적인 기울기 계산의 핵심
수치 미분은 단순하고 구현이 쉽지만 계산 시간이 오래 걸린다는 치명적인 단점이 있다. 이를 해결하기 위해 가중치 매개변수의 기울기를 효율적으로 계산하는 오차역전파법(Backpropagation)을 사용한다. 이 강력한 알고리즘을 계산 그래프를 통해 직관적으로 이해해보자.
계산 그래프: 시각적 계산의 도구
계산 그래프란?
계산 그래프는 계산 과정을 노드(원)와 에지(화살표)로 표현한 그래프다. 복잡한 계산을 시각적으로 분해하여 이해하기 쉽게 만든다.
계산 그래프로 문제 풀기
문제 1: 사과 쇼핑
현빈군은 슈퍼에서 1개에 100원인 사과를 2개 샀다. 소비세가 10% 부과될 때 지불 금액을 구해보자.
계산 그래프로 풀어본 문제 1의 답
계산 그래프 구성 요소:
- 노드: 원으로 표기하고 연산 내용을 적는다
- 에지: 화살표로 계산 결과가 왼쪽에서 오른쪽으로 전달됨을 나타낸다
- 순전파: 왼쪽에서 오른쪽으로의 계산 흐름
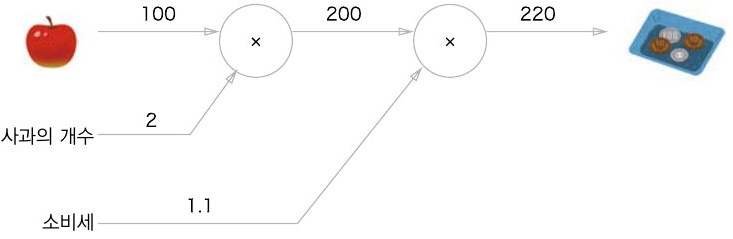사과의 개수’와 ‘소비세’를 변수로 취급해 원 밖에 표기
문제 2: 복합 쇼핑
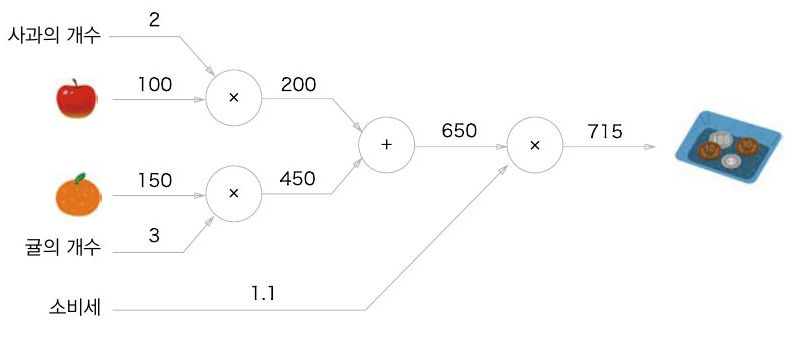
현빈군은 사과를 2개, 귤을 3개 샀다. 사과는 1개에 100원, 귤은 1개에 150원이다. 소비세가 10%일 때 지불 금액을 구해보자.
계산 그래프로 풀어본 문제 2의 답
더 복잡한 계산에서도 계산 그래프는 체계적으로 문제를 해결할 수 있다.
국소적 계산의 힘
국소적 계산이란?
계산 그래프의 핵심 특징은 국소적 계산을 전파하여 최종 결과를 얻는다는 점이다.
국소적 계산의 특징:
- 자신과 직접 관계된 작은 범위만 고려한다
- 전체에서 무슨 일이 일어나든 상관없이 자신의 역할만 수행한다
- 각 노드는 자신과 관련한 계산 외에는 신경 쓸 필요가 없다
계산 그래프의 장점
1. 문제 단순화
전체가 아무리 복잡해도 각 노드에서는 단순한 계산에만 집중하면 된다.
2. 중간 결과 보관
모든 중간 계산 결과를 보관할 수 있어 디버깅과 분석이 용이하다.
3. 효율적인 미분 계산
가장 중요한 장점으로, 역전파를 통해 미분을 효율적으로 계산할 수 있다.
역전파에 의한 미분 값의 전달
역전파의 의미:
- 순전파와 반대 방향(오른쪽에서 왼쪽)으로 진행
- 사과 가격에 대한 지불 금액의 미분을 구한다
- 미분 값은 사과 값이 조금 올랐을 때 최종 지불 금액의 증가량을 나타낸다
- 여러 변수에 대한 미분을 동시에 효율적으로 계산할 수 있다
연쇄법칙: 역전파의 수학적 원리
연쇄법칙이란?
연쇄법칙은 합성함수의 미분에 대한 성질이다.
합성함수 예시
\(z = t^2\)
\(t = x + y\)
이때 z는 x와 y의 합성함수다.
연쇄법칙 공식
\(\frac{\partial z}{\partial x} = \frac{\partial z}{\partial t} \frac{\partial t}{\partial x}\)
의미: 합성함수의 미분은 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
계산 예시:
- $\frac{\partial z}{\partial t} = 2t$
- $\frac{\partial t}{\partial x} = 1$
- 따라서 $\frac{\partial z}{\partial x} = 2t \times 1 = 2(x+y)$
연쇄법칙과 계산 그래프
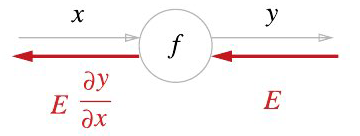순전파와는 반대 방향으로 국소적 미분을 곱해 전달한다.
역전파의 원리:
- 순전파와 반대 방향으로 국소적 미분을 곱해서 전달
- 가장 왼쪽의 역전파 신호는 최종적으로 $\frac{\partial z}{\partial x}$가 된다
- 역전파가 하는 일이 연쇄법칙의 원리와 정확히 일치한다
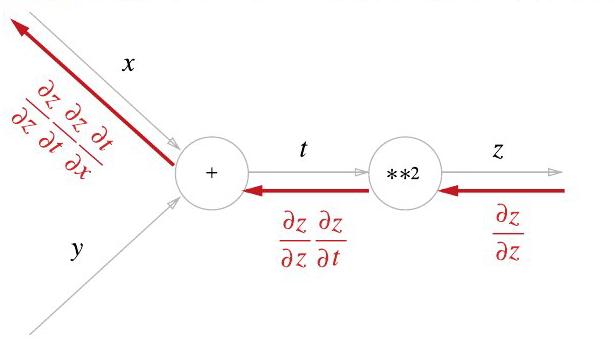계산 그래프의 역전파: 순방향과는 반대 방향으로 국소적 미분을 곱한다.
기본 연산의 역전파
덧셈 노드의 역전파
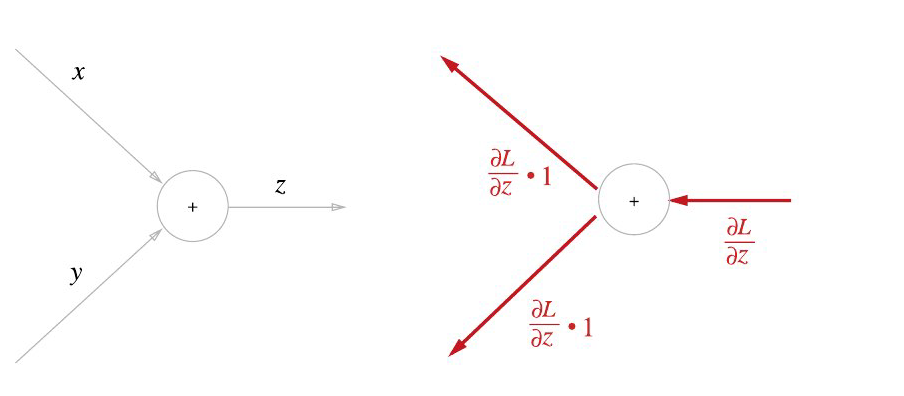덧셈 노드 역전파는 입력 신호의 값을 다음 노드로 그대로 출력한다.
덧셈 노드의 특징:
- 역전파에서 입력 신호를 그대로 다음 노드로 전달
- 수학적 근거: $\frac{\partial}{\partial x}(x + y) = 1$, $\frac{\partial}{\partial y}(x + y) = 1$
- 상류에서 온 미분값을 변화 없이 하류로 전달
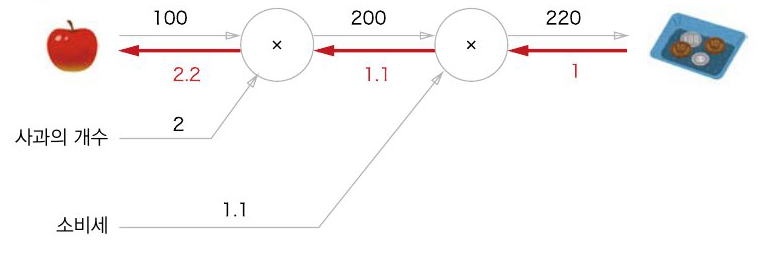
곱셈 노드의 역전파
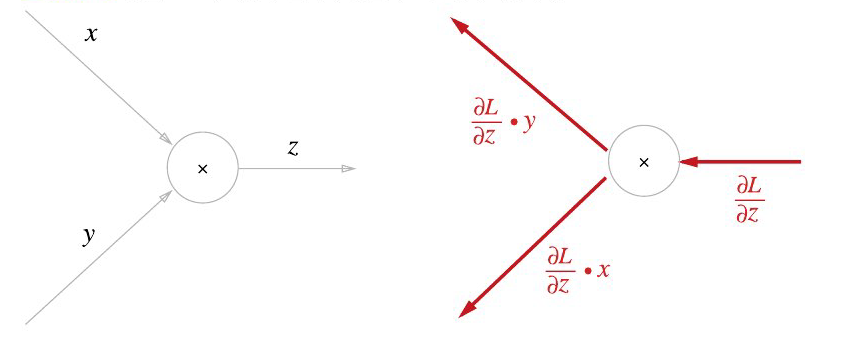곱셈 노드 역전파는 입력 신호들을 서로 바꾼 값을 곱해 하류로 보낸다.
곱셈 노드의 특징:
- 순방향 입력 신호들을 서로 바꾼 값을 곱해서 하류로 전달
- 수학적 근거: $\frac{\partial}{\partial x}(xy) = y$, $\frac{\partial}{\partial y}(xy) = x$
- 중요: 곱셈 노드는 순전파의 입력 신호 값이 필요하므로 저장해둬야 한다
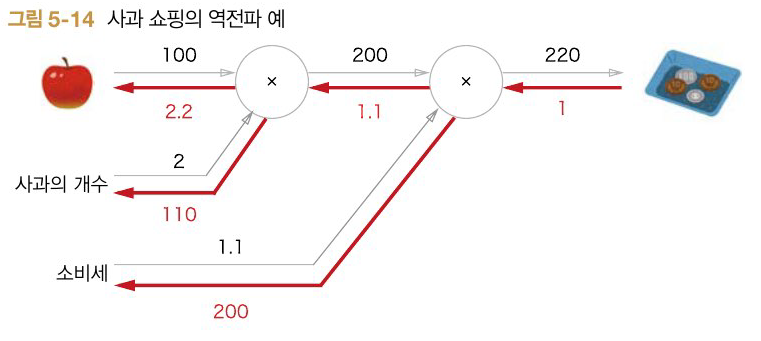
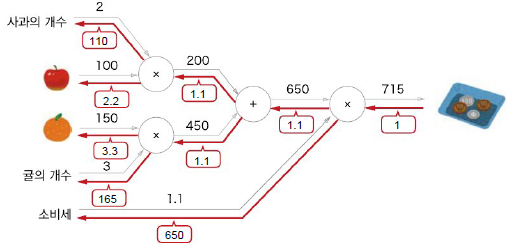
사과 쇼핑 예시의 완전한 역전파
결과 해석:
- 사과 가격에 대한 미분: 2.2 (사과 가격이 1원 오르면 총액이 2.2원 증가)
- 사과 개수에 대한 미분: 110 (사과 1개 추가하면 총액이 110원 증가)
- 소비세에 대한 미분: 200 (소비세가 0.01 오르면 총액이 2원 증가)
문제 2 또한 표현 할 수 있다.
역전파 계산 과정:
- 최종 출력에서 시작하여 각 노드의 국소적 미분을 계산
- 상류에서 전달받은 미분값에 국소적 미분을 곱해서 하류로 전달
- 각 변수에 대한 최종 미분값을 효율적으로 구할 수 있다
마무리
오차역전파법은 계산 그래프와 연쇄법칙을 기반으로 한 효율적인 미분 계산 방법이다. 수치 미분과 달리 정확하면서도 빠르게 기울기를 계산할 수 있어 신경망 학습의 핵심 기술이 되었다.
핵심 포인트:
- 계산 그래프: 복잡한 계산을 시각적으로 분해
- 국소적 계산: 각 노드는 자신의 역할만 수행
- 연쇄법칙: 합성함수 미분의 수학적 원리
- 역전파: 효율적인 기울기 계산의 핵심
다음 단계에서는 이 원리를 실제 신경망의 각 층(활성화 함수, 손실 함수 등)에 적용하여 완전한 오차역전파법을 구현하는 방법을 살펴보겠다.